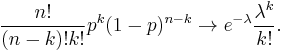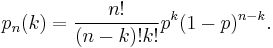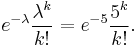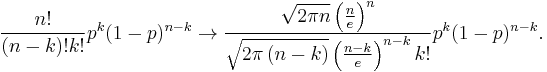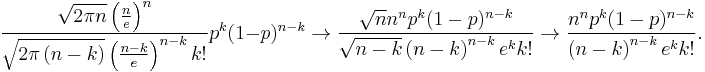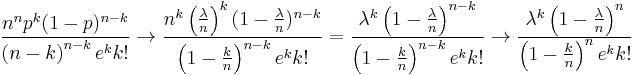Poisson limit theorem

The Poisson theorem gives a Poisson approximation to the binomial distribution, under certain conditions.[1] The theorem was named after Siméon-Denis Poisson (1781–1840).

Contents

The theorem

If

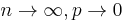n \rightarrow \infty, p \rightarrow 0, such that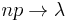 np \rightarrow \lambda

then

\frac{n!}{(n-k)!k!} p^k (1-p)^{n-k} \rightarrow e^{-\lambda}\frac{\lambda^k}{k!}.

Example

Suppose that in an interval of length 1000, 500 points are placed randomly. Now what is the number points that will be placed in a sub-interval of length 10? If we look here, the probability that a random point will be placed in the sub-interval is 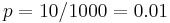p = 10/1000 = 0.01. Here 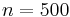n=500 so that 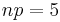np=5. The probabilistically precise way of describing the number of points in the sub-interval would be to describe it as a binomial distribution 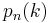p_n(k). That is, the probability that 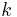k points lie in the sub-interval is

p_n(k)=\frac{n!}{(n-k)!k!} p^k (1-p)^{n-k}.

But using the Poisson Theorem we can approximate it as

e^{-\lambda}\frac{\lambda^k}{k!} = e^{-5}\frac{5^k}{k!}.

The proof

Accordingly to factorial's rate of growth, we replace factorials of large numbers with approximations:

\frac{n!}{(n-k)!k!} p^k (1-p)^{n-k} \rightarrow \frac{ \sqrt{2\pi n}\left(\frac{n}{e}\right)^n}{ \sqrt{2\pi \left(n-k\right)}\left(\frac{n-k}{e}\right)^{n-k}k!} p^k (1-p)^{n-k}.

After simplifying the fraction:

\frac{ \sqrt{2\pi n}\left(\frac{n}{e}\right)^n}{ \sqrt{2\pi \left(n-k\right)}\left(\frac{n-k}{e}\right)^{n-k}k!} p^k (1-p)^{n-k}\rightarrow \frac{ \sqrt{n}n^np^k (1-p)^{n-k}}{ \sqrt{n-k}\left(n-k\right)^{n-k}e^kk!}\rightarrow \frac{n^np^k (1-p)^{n-k}}{\left(n-k\right)^{n-k}e^kk!}.

After using the condition 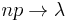np \rightarrow \lambda:

\frac{n^np^k (1-p)^{n-k}}{\left(n-k\right)^{n-k}e^kk!} \rightarrow \frac{n^k\left(\frac{\lambda}{n}\right)^k (1-\frac{\lambda}{n})^{n-k}}{\left(1-\frac{k}{n}\right)^{n-k}e^kk!}=\frac{\lambda^k \left(1-\frac{\lambda}{n}\right)^{n-k}}{\left(1-\frac{k}{n}\right)^{n-k}e^kk!}\rightarrow\frac{\lambda^k \left(1-\frac{\lambda}{n}\right)^{n}}{\left(1-\frac{k}{n}\right)^{n}e^kk!}

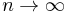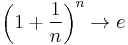Apply, that due to n\rightarrow \infty we get \left(1%2B\frac{1}{n}\right)^n \rightarrow e:

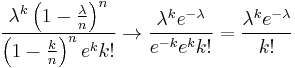
\frac{\lambda^k \left(1-\frac{\lambda}{n}\right)^{n}}{\left(1-\frac{k}{n}\right)^{n}e^kk!}\rightarrow\frac{\lambda^k e^{-\lambda}}{e^{-k}e^kk!}=\frac{\lambda^k e^{-\lambda}}{k!}

Q.E.D.

See also

References

  1. ^ Papoulis, Pillai, Probability, Random Variables, and Stochastic Processes, 4th Edition